Numerical Methods Helper

The full source code for my numerical methods helper is now available on the GitHub repository.

Download the User Manual

Download the executable

Numerical Methods Helper is a learning tool for numerical algorithms in AS and A2 Mathematics modules. The program supports methods of numerical integration, root finding through iteration, local extrema, and tangents and normal lines to functions.

The progress of each algorithm is drawn onto a freely movable and interactive graph to allow students the most engaging learning experience. All parameters for each algorithm are completely customisable, and the results and graphs will be re drawn to accommodate the new values.

Not only does Numerical Methods Helper give a final result to an algorithm, but it also gives the calculations needed for students to get the final answer for themselves. For example, all integration algorithms are accompanied with list of ordinates used in the algorithm, along with a final formula that can be typed into any calculator to yield the final same final result.

Functions for use in any of the algorithms can be freely customised and changed using a number of built operators including trigonometry and logarithms. Not only can the program be used for the tuition of numerical methods, but the graphs can also be utilised for other topics such as transformations of graphs.

Main Features -

• Freely scrollable and zoomable graphing view
• Worked examples of all numerical algorithms and AS and A2 Maths including -
  • The Trapezium rule
  • The Mid - Ordinate Rule
  • Simpsons Rule
  • Root Finding by iteration
• Teaching aids for other topics such as local extrema and tangents and normal lines to functions
• Every parameter for each algorithm is fully customisable to meet a wide range of questions
• Functions for use in any algorithm can be changed using a wide range of built in operators
• Graphing views can be copied to the clipboard to paste into other applications for annotation and printing
• Main parameters for algorithms can be modified by dragging points on the graph itself. This allows for a more interactive and visual approach to the progress and inaccuracies of the algorithm
• Numerical data used in the calculations of the results of the algorithm is also provided to allow students themselves to reach a solution

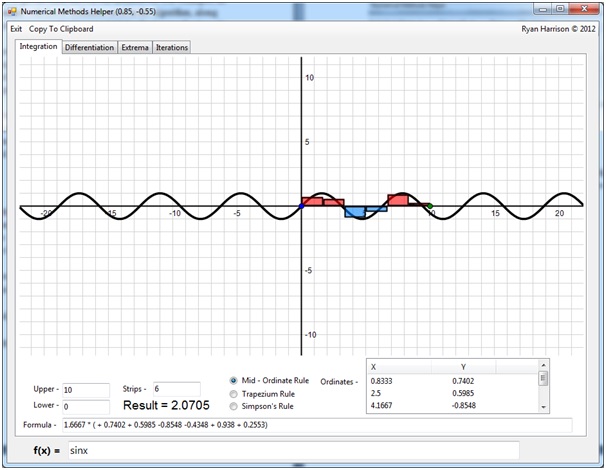
This screenshot shows the integration tab of the program. The user is able to enter a custom function along with the upper and lower bounds of the integration, the numerical algorithm to use and the number of iterations. The results are then shown to the user, with a formula of the chosen algorithm and the ordinates used. Te application of the algorithm to the equation is also shown graphically on an interactive plotting view.

For more information about the application, download the User Manual along with the executable from GitHub or as a zip file.